Inertia

We know that mass exibits inertia, that is, there's a resistance to accelerating mass, and that once accelerated, there's resistance to slowing mass down.

This concept can be explained by looking at the energy in the system. Called kenetic energy, it's expressed as:

    e = 1/ 2 * mass * velosity-squared

It shows up in the real world in a number of ways, that include:

1. Different falling masses accelerate at the same rate

It was once though that heavier objects would fall faster, but this is not the case. Although larger masses have stronger forces (heavier), they must have something that holds them back, as they accelerate in a gravitational field. This force seems to be directly related to their mass, or, more specifically, is a second propery of mass.

2. It does take energy to accelerate. A common example is the automobile. You burn gas to accelerate, but then once rolling, and without resistance, you'd keep going forever. Where does this energy go when I accelerate?

3. You must remove energy to decelerate. Continuing with the car, you can hit the brakes, which dissapate the kenetic energy as heat. But, again, where does this energy come from when I decelerate?

----

Lets take a closer look at acceleration.

Since we need some accleration to get some velosity in the first place, the math states:

    velosity = acceleration * time

If we look at the acceleration term, from the unatom's point of view, we were at rest with a center of mass at one point, but then suddenly, we are at some new point.

It's already been conjectured that an unatom consists of a gauge, or field surrounding the center of mass.

Further, lets conjecture that this field travels with the unatom.

But lets add a new conjecture, that there's a radiation out from the unatom whenever it accelerates. And, lets give this radiation some  rapid velosity, V - probably in the range of C, the speed of light.

Now, lets also conjecture that this radiation interacts with the gauge surrounding the unatom, in such a way as to resist the atoms new position (acceleration). Think of it as a back pressure trying to slow the unatom down and keep it in position.

This radiation must travel out and readjust the gauge to the new position of the unatom.

Doing so requires energy.

Further, the radiation is traveling out at V/C?, and we know that as it travels out, it becomes weaker, as a matter of fact 1/r^2, where r is the distance out from the unatom - and that, at some point, becomes insignificant.

---

Well, it explains the back pressure as a function of mass - something that's needed to explain why heavier bodies don't fall faster.

The conjecture shows where kenetic energy can be stored.

It explains why the forces act only on acceleration. Once an object settles on a new velosity, V/C? has carried the radiation out so far its forces are negligble.

---

Here's world9 that demonstrates the interaction of the gauge and the radiation: world9.tar.bz2.

Here's it's screen shot:



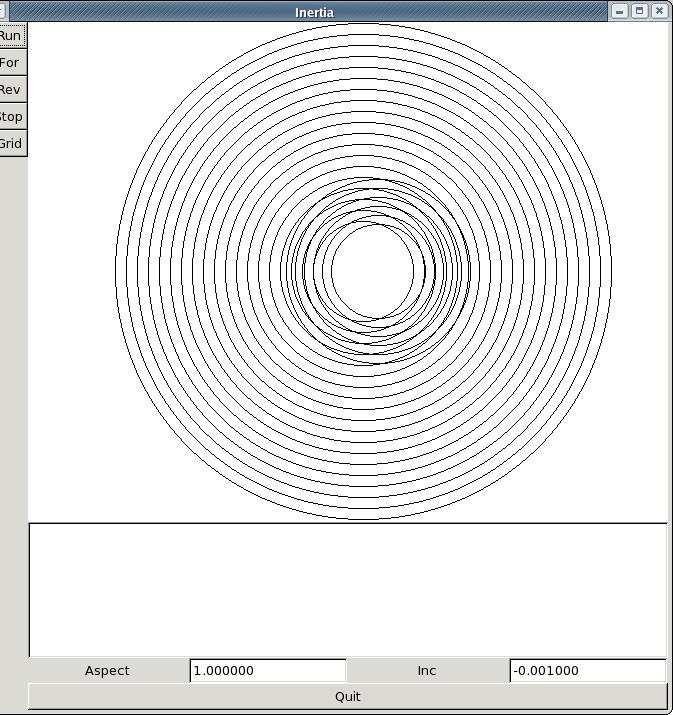
You are looking at one unatom that has been accelerated to the right. The larger set of concentric circles represent its origional position, and the smaller set its new position.

The slightly asymetrical gauge represents the inertial back pressure.

World9 supports the following buttons:

Run - causes the new position unatom radiation to propogate to the edge of the screen. Then, the simulation is stopped.

For - step the radiation propogation one outward.

Rev - step the radiation propogation one inward.

---

It's interesting to note you see more asymetric fields if the wavelength of the unatoms new position is different from that of it's stationary position. I don't have an answer for this yet.